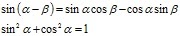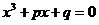Trigonometrijske funkcije dvostrukog ugla - zadatak 1

Dokazati da je

Iz  adicionih teorema ćemo izvesti izraze za sin i cos dvostrukog ugla

Iz čega sledi da je

Analitička geometrija – prava- primer 3

Tačke A(-3,-1), B(1,1) i C(-2,3) određuju trougao. Napisati jednačinu pravih na kojoj leže visina i težišna linija iz temena C. Odrediti podnožje visine iz temena C i dužinu ove visine.

Prvo ćemo nacrtati skicu

Pođimo od visine. Vidimo da prava na kojoj leži visina prolazi kroz tačku C i normalna je na pravu p na kojoj leži duž AB. Iz toga zaključujemo da ćemo jednačinu prave na kojoj leži visina naći iz jednačine prave kada je poznata jedna tačka i koeficijent pravca .

Kardanova formula - primer 2

Rešiti kubnu jednačinu

Prva smena nije potrebna jer smo već dobili jednačinu oblika

Gde je

Da bi smo doredili broj i tip rešenja tražimo diskriminantu D

Diskriminanta je veća od nule, što znači da ćemo imati realna rešenja, od kojih je bar jedno dvostruko.
Kada je diskriminanta veća ili jednaka nuli, koristimo Kardanove formule

Adicione teoreme - zadatak 2

Osnovnatrigonometrijska funkcija tg je

Iz adicionih teorema (koje treba naučiti napamet)

Sledi da je

Trigonometrijski krug - zadatak 4

Uprosti izraz:

Sve se zasniva na crtanju trigonometrijskog kruga i ništa se ne mora učiti napamet

Adicione teoreme - zadatak 1

Iz adicionih teorema (koje treba naučiti napamet) znamo da je

Prema postavci zadatka, nacrtamo kako izgledaju uglovi u trigonometrijskom krugu

Trigonometrijski krug - zadatak 3

Poznavanje trigonometrijskog kruga je osnov za savladavanje trigonometrije. Njegovim korišćenjem, uz poznavanje trigonometrijskih transformacija , svaki zadatak iz oblasti trigonometrije postaje lak za rešavanje.
To ćemo ilustrovati na nekoliko primera

Uprosti izraz:

Znamo da su trigonometrijske funkcije periodične, i to

Trigonometrijski krug - zadatak 2

Poznavanje trigonometrijskog kruga je osnov za savladavanje trigonometrije. Njegovim korišćenjem, uz poznavanje trigonometrijskih transformacija , svaki zadatak iz oblasti trigonometrije postaje lak za rešavanje.

To ćemo ilustrovati na nekoliko primera

Uprosti izraz

Znamo da su trigonometrijske funkcije periodične, i to

Trigonometrijski krug - zadatak 1

Poznavanje trigonometrijskog kruga je osnov za savladavanje trigonometrije. Njegovim korišćenjem, uz poznavanje trigonometrijskih transformacija , svaki zadatak iz oblasti trigonometrije postaje lak za rešavanje.
To ćemo ilustrovati na nekoliko primera

Uprostiti izraz

Rešavamo  zadatak korak po korak.

Na slici , na trigonometrijskom krugu, vidimo koje dužine predstavljaju osnovne trigonometrijske funkcije

Kubna jednačina, jednostavna za rešavanje

Rešiti kubnu jednačinu

Ovde imamo  kubnu jednačinu oblika

U kojoj je

Kubna jednačina - primer rešavanja trigonometrijskom metodom 2

Rešiti kubnu jednačinu

Ovde većimamo  kubnu jednačinu oblika

U kojoj je

te nije potrebno uvoditi prvu smenu
Zato odmah tražimo diskriminantu,da bi smo odredili broj i tip rešenja

Kardanova formula - primer

Rešiti kubnu jednačinu:

Jednačina je oblika

Uvodimo prvu smenu

Kubna jednačina - primer rešavanja trigonometrijskom metodom 1

Rešiti kubnu jednačinu

Ovde većimamo  kubnu jednačinu oblika

U kojoj je

te nije potrebno uvoditi prvu smenu
Zato odmah tražimo diskriminantu,da bi smo odredili broj i tip rešenja

Kubna jednačina - primer

Rešiti kubnu jednačinu

Uvodimo prvu  smenu

Kubna jednačina

Polinom (a ≠ 0) trećeg stepena (1):

seče X-osu u tačkama koje su nule odgovarajuće jednačine trećeg stepena, kubne jednačine 

Prva smena

Jednačina (a ≠ 0) trećeg stepena (3):