Adicione teoreme

Moraju se znati napamet

 1.Ako su

koliko je

Iz prvog uslova sledi da je

S obzirom da je

Kada zamenimo vrednosti dobijamo da je

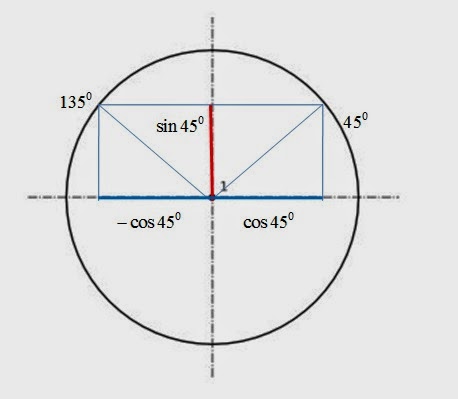
Iz trigonometrijskog kruga vidimo da je

Važna napomena: Kad god je moguće izvršiti racionalizaciju i ne ostavljati koren u imeniocu.

3. Rešiti jednačinu

 

Iz trigonometrijskih kružnica vidimo da je

4. Rešiti jednačinu

Cilj nam je da jednačinu pretvorimo u oblik koji će sadržati samo jednu trigonometrijsku funkciji i jedan ugao.

Iz trigonometrijskih kružnica vidimo da je

 

5. Dokazati da je

Algebarski izrazi

Podelimo i brojioc i imenioc sa cosx

Osnovne trigonometrijske funkcije

Osnovne trigonometrijske funkcije-zadaci
Trigonometrija - zadaci za vežbu
Trigonometrijski krug - zadatak 1
                                     - zadatak 2
                                     - zadatak 3
                                     - zadatak 4
Adicione teoreme - zadatak 1
                              - zadatak 2
                              - zadatak 3
Trigonometrijske funkcije dvostrukog ugla - zadatak 1
                                                                      - zadatak 2
                                                                      - grupa zadataka 1
                                                                      - grupa zadataka 2
Trigonometrijske jednačine - zadatak 1
                                             - zadatak 2
                                             - zadatak 3
                                             - zadatak 4

Pitajte i dobićete odgovor

Izvor zadataka:  Zorica Uzelac, Nevenka Adžić, Rade Doroslovački- Priprema za prijemni ispit iz matematike, 2003