Prvo moramo odrediti definisanost izraza.
Racionalna funkcija je
definisana ako i samo ako je imenilac različit od nule.
Izraz
je definisan za
Ova
funkcija će biti veća od 0 (pozitivna) kada su brojilac i imenilac istog znaka,
a jednaka 0 kada je brojilac 0.
Zato
ćemo posebno nacrtati funciju u brojiocu i funkciju u imeniocu i odrediti im
znake.
Funkcija
Ima korene -2 i 1, a pošto
je a=-1<0, okrenuta je otvorom na dole
Funkcija
je
prava linija
koja
seče y osu u tački (0,-6)
i
x osu u tački (6,0)
Nejednačine sa racionalnim funkcijama - primer 2
Nejedna;ine sa racionalnim funkcijama - primer 3
Nejednačine sa racionalnim funkcijama - primer 4
Linearne i kvadratne jednačine-zadaci
jednačina sa apsolutnim vrednostima i diskusijom parametra
Nejedna;ine sa racionalnim funkcijama - primer 3
Nejednačine sa racionalnim funkcijama - primer 4
Linearne i kvadratne jednačine-zadaci
jednačina sa apsolutnim vrednostima i diskusijom parametra








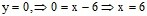




Нема коментара:
Постави коментар