Rešiti
jednačine:
Ovo
je eksponencijalna jednačina jednačina i prvo je moramo urediti tako da osnove
budu jednake.
Izvršićemo
smenu, tako da dobijemo kvadratnu jednačinu.

Rešenje
t1
ne
zadovoljava uslov definisanosti eksponencijalne jednačine pa je
Prvo
moramo dovesti logaritme na istu osnovu.(Osobine logaritma)
Izvršićemo
smenu, tako da dobijemokvadratnu jednačinu.
Koristeći
pravila stepenovanja i korenovanja, prvo ćemo srediti jednačinu
Jednačina
je tačna za svako x koje pripada
skupu realnih brojeva.
4.
Rešiti nejednačinu
Jednačina
ima smisla ako je
Sada
ćemo srediti eksponencijalnu jednačinu dovodeći članove na istu osnovu
Pošto
je
Izraz
će biti manji od nule ako su linearne funkcije u brojiocu i imeniocu različitog
znaka.
Odredićemo
znak ovih linearnih funkcija

Rešenje
nejednačine je
U
ovom slučaju imamo jednačinu sa prirodnim logaritmom čija je osnova broj e.
Jednačina
ima smisla ako je
Koristeći
osobine logaritma sredićemo jednačinu
Rešićemo
kvadratnu jednačinu
Pa
je rešenje jednačine
6.
Za koje vrednosti parametra m jednačina ima
realne korene
Jednačina
će imati realne korene ako je diskriminanta kvadratne funkcije veća ili jednaka
nuli
7.
Rešiti sistem jednačina
Sistem
ima smisla ako su
Prvo
ćemo dovesti logaritme na istu osnovu, a zatim dalje rešavati sistem
Rešenje
sistema je skup uređenih parova
Eksponencijalne nejednačine - zadaci
Eksponencijalne jednačine - primer 1
Eksponencijalne jednačine - primer 2
Eksponencijalne jednačine - primer 3
Logaritamske jednačine
Osobine logaritama- primena u zadacima
Logaritamske nejednačine
Sistem logaritamskih jednačina
Logaritamska i kubna jednačina u jednom zadatku
Pitajte i dobićete odgovor!
Eksponencijalne jednačine - primer 1
Eksponencijalne jednačine - primer 2
Eksponencijalne jednačine - primer 3
Logaritamske jednačine
Osobine logaritama- primena u zadacima
Logaritamske nejednačine
Sistem logaritamskih jednačina
Logaritamska i kubna jednačina u jednom zadatku
Pitajte i dobićete odgovor!














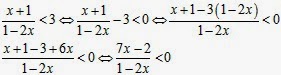
















Нема коментара:
Постави коментар