Linearne i kvadratne jednačine i nejednačine-zadaci za vežbu

                                              1.Odrediti m tako da jednačina  ima realna i različta rešenja.

                       

     Kvadratna jednačina ima realna i različita rešenja, ako je diskriminanta D>0.

     Kvadratne jednačine i nejednačine

     Algebarski izrazi

    

    Treba da odredimo vrednosti m za koje je funkcija D veća od nule.

    

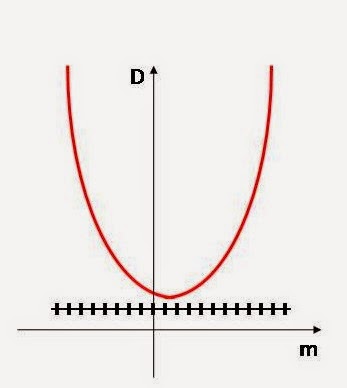
Funkcija D nema rešenja u skupu realnih brojeva, a pošto je a=1, okrenuta je sa otvorom na gore.

    Sa slike vidimo da je pozitivna za svako m koje pripada skupu realnih brojeva.

Rešenje:  

2.    Odrediti x za koje je 

Prvo ćemo srediti nejednačinu.

   a onda određujemo kada je izraz definisan.

   Racionalni izraz je definisan ako je imenilac različit od 0.

Uslovi nejednakosti

     će biti ispunjeni ako su i brojilac i imenilac istog znaka.

     Odredićemo znakove funkcija u brojiocu i imeniocu.

     Kvadratne jednačine i nejednačine

Kako je a=1>0, to je funkcija okrenuta sa otvorom na gore.

I u ovoj funkciji je a=1>0, pa je i ona okrenuta sa otvorom na gore.

Rešenje nejednačine

    3.Rešiti sistem nejednačina

Sistem jednačina sa apsolutnim vrednostima

Prema definiciji apsolutne vrednosti je:

Apsolutna vrednost

Zato moramo razmatrati 4 slučaja

Rešenje je skup uteđenih parova

4. Rešiti jednačinu

Jednačine sa apsolutnim vrednostima

Prema definiciji apsolutne vrednosti je

Apsolutna vrednost

Zbog toga moramo prvo da odredimo znak obe funkcije

Kvadratne jednačine i nejednačine

Parabola je okrenuta sa orvorom na gore, jer je a=1>0.

I ova parabola je okrenuta sa otvorom na gore, a=1>0.

Mogu se prihvatiti samo ona rešenja koja zadovoljavaju početni uslov, pa je rešenje

Algebarski izrazi

Ni jedno rešenje ne zadovoljava početni uslov.

Konačno rešenje jednačine je skup svih rešenja

5.Napisati kvadratnu jednačinu čiji su koreni za 5 veći od korena jednačine

Prvo moramo naći korene date jednačine

Kvadratne jednačine i nejednačine

Iz uslova zadatka su koreni tražene jednačine

Traženu jednačinu ćemo dobiti iz oblika

6.Rešiti sistem jednačina

Ako saberemo ove 2 jednačine dobićemo kvadratnu jednačinu po x

Nepoznatu y ćemo dobiti kada dobijene vrednosti za x uvrstimo u jednu od jednačina. Uvrstićemo u drugu.

Rešenje sistema je skup uređenih parova

7.Rešiti jednačinu

Jednačinu možemo napisati i u obliku

Stepenovanje i korenovanje

Pa uvodimo smenu

Rešenje jednačine je skup

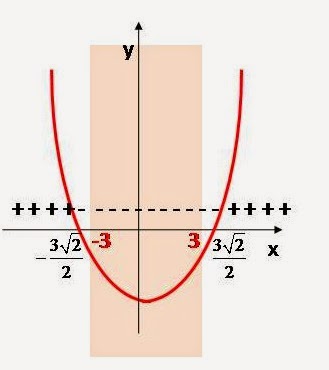
                                    8.Rešiti nejednačinu

Prvo određujemo definisanost izraza.

Parni koren je definisan ako je podkorena veličina veća ili jednaka 0.

Ovaj izraz je definisan za

Ovo je kvadratna funkcija i prvo joj određujemo znak.

Kvadratne jednačine i nejednačine

Pošto je a=-1<0 to je parabola okrenuta sa otvorom na dole.

    Izraz je definisan za

 

     

   Da bismo se oslobodili korena kvadriraćemo nejednačinu

Određujemo znak kvadratne funkcije

   Funkcija je manja od 0 ako

    

  Ali obe vrednosti izlaze iz oblasti definisanosti, pa je rešenje nejednačine

     

Pitajte, odgovorićemo

Operacije sa algebarskim izrazima

Linearne jednačine i nejednačine

Izvor zadataka:  Zorica Uzelac, Nevenka Adžić, Rade Doroslovački- Priprema za prijemni ispit iz matematike, 2003